La gráfica de las funciones polinómicas depende del grado de la función. Las funciones polinómicas de ciertos grados tienen ciertas alternativas de gráfica. Queda a este curso de derivadas averiguar algunas de las características de las funciones para poder predecir su comportamiento.
Muchas veces a partir de la gráfica de un polinomio se puede deducir la ecuación de la función. Ésto se puede hacer a partir de las intersecciones con los ejes. (Conste que comenté, que muchas veces, NO SIEMPRE).
Una función polinómica con el más alto número de intersecciones con el eje "x" permisible, es aquella que se puede determinar su gráfica y su ecuación.
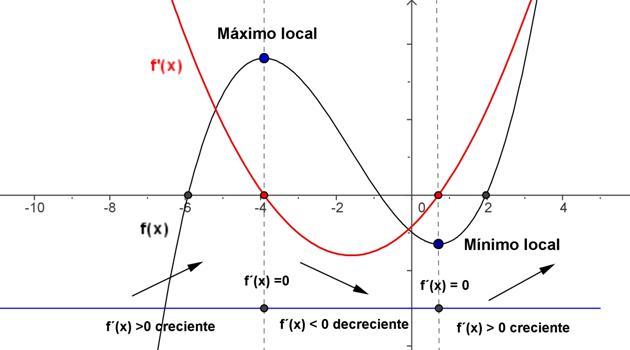
INTERVALO CRECIENTE Y DECRECIENTE
Funcion descreciente
Si f es decreciente en a si sólo si existe un entorno de a, tal que para toda x que pertenezca la entorno de a se cumple:
Si f es derivable en a:
Función creciente
Si f es creciente en a si sólo si existe un entorno de a, tal que para toda x que pertenezca la entorno de a se cumple:
Si f es derivable en a:
No hay comentarios:
Publicar un comentario